Convolution visualization 2156

by Matthew Baas

A quick post connecting the ideas of the convolution operation in mathematics & signals analysis to deep learning convolution.

TL;DR: How does the systems & signals idea of convolution relate to convolution in deep learning?

Convolution in systems and signals is an operation of a function \(h(t)\) with another function \(x(t)\), denoted as \(y(t) = h(t) * x(t)\) defined by the integral:

Convolution in deep learning is a discrete convolution operation applied over several input channels (discrete input functions) with the convolving function not flipped.

Convolution in systems and signals

The core definition of convolution was given above. In analysis of systems and signals, the convolution operation is used to find the output of linear time invariant systems when information about the system (the impulse response) is known. When used this way, \(h(t)\) is known as the impulse response or weighting function, \(x(t)\) is the input signal, and \(y(t)\) is the output signal. Thus the output signal is given by convolving the input signal \(x\) with the weighting function \(h\).

A good example demonstrates this integral’s action:

Say we have a function \(h(t) = 2e^{-t/2}\) and we want to convolve it with another function \(x(t)\), defined as:

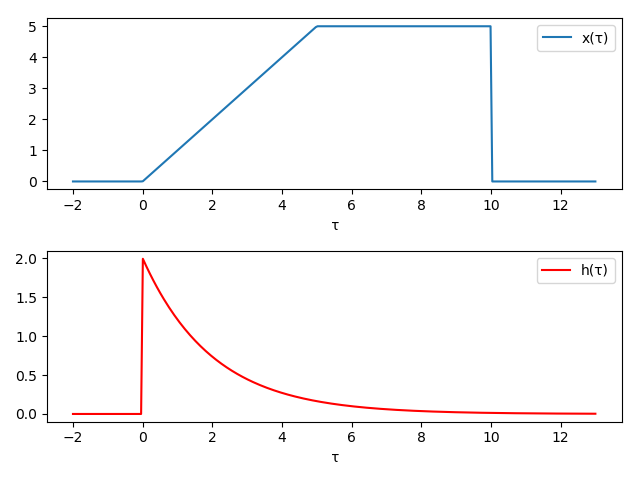
Now \(x(t-\tau)\) is just the function reflected over the y-axis and shifted rightward by \(t\).

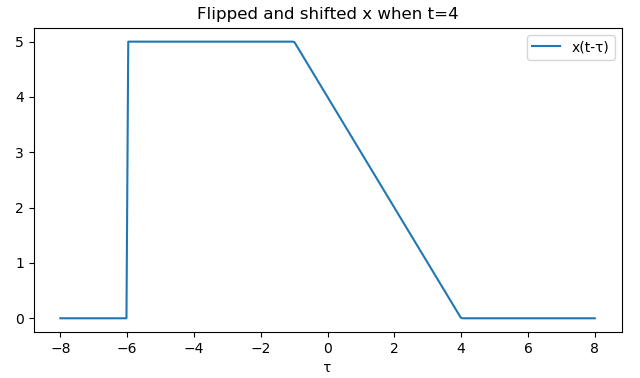
So, now looking at the integral, \(y(t)\) is the total area under the multiplication of the functions, giving in a sense a measure of the overlapping area of the two functions. So seeing this operation in action, let’s show how the value of \(y(t)\) (in green) is computed as we change \(t\) from -2 to 15. Again, remember that at each value for \(t\), \(y(t)\) is the _area under the function \(h(\tau)x(t - \tau)\) over all \(t\).

Note that the convolving function can be swapped without changing the result – i.e \(x(t) * h(t) = h(t) * x(t)\).

Convolution in deep learning

Now going into the details of how deep learning convolution is related to the standard mathematical convolution:

1. Deep learning convolution is discrete

As is fairly common when dealing with integrals, when the functions \(h(t)\) and \(x(t)\) are no longer continuous but discrete and only defined for certain values of \(t\) (e.g \(t\) can only be natural numbers, corresponding to indices of values in an array), then the integral sign becomes a summation sign and we slide the convolving function \(x(t-\tau)\) in discrete steps instead of a continuous motion. In the previous example, say now the given functions were only defined for discrete values for \(t\), then the animation would look like:

2. Deep learning convolution is applied over several input functions

For now let’s say we have a 1 dimensional color image, stored as three 1D array of numbers, one array for red, green, and blue. These 3 different sets of numbers are called the channels of the convolution. Now for convolution in deep learning, we use the same discrete weighting function \(h\) to convolve with all 3 of these channels where, at each value of \(t\) (the discrete index), we sum the results of the defining convolution integral of \(h\) and the channels together to obtain the output \(y\).

Continuing with the running example, say we have a second input channel with a function \(k(t)\) defined as below:

Then the process of summing the output of the convolution of both channels gives us a process like:

Another difference between the two ideas of convolution that needs clarification is the mirroring/flipping of the convolving function about the y-axis:

3. Deep learning convolution does not flip the convolving function

This is to say that instead of taking \(h(t-\tau)\) (or equivalently \(x(t-\tau)\)), we do not flip the function and just shift it – i.e we instead just use \(h(\tau - t)\). Now this may seem odd, but as using the same value/function for \(h\) will not give the same result when convolved in these two different ways. The reason for doing this is that in convolutional neural networks, we aim to find a value for the weighting function \(h\) through training, where we have an indication of the input and output (the training data), whereas in other applications we usually know something about \(h\) and the input and want to find the output.

So, since we are finding an \(h\) that matches a set of specifications, whether it is flipped or not is irrelevant. If we solved/trained for \(h(t)\) using the non-flipped version, it would correspond to a solution for \(h(t)\) using the flipped operation! Phrased differently, using the non-flipping operation just means the \(h(t)\) we find is the flipped version of \(h(t)\) we would find with the normal convolution operation, and since (with the normal operation) we would only ever use the \(h(t)\) when it is flipped inside the integral, finding its flipped version initially and not flipping it inside the integral/sum is equivalent.

So ultimately, since in deep learning we want to find an \(h(t)\), both methods give valid and corresponding solutions. We simply pick the non-flipping method since it is less computational work to just keep the flipped \(h\) instead of the original \(h\) and flip it each time we want to do a sum.

4. Deep learning convolution usually is done over multiple dimensions

In the running example we have shown convolution in 1D with functions of single variables, but deep learning convolution is often used with image or even volumetric data, where \(t\) is no longer a single value but a 2- or 3-tuple, containing the coordinates of a pixel/voxel in 2D/3D. This does not change the process significantly, the functions \(x(t)\), and \(h(t)\) are now defined over a grid (or volume) of possible \(t\) tuples. And again remember point 2., that the weighting function \(h(t)\) is usually convolved with several inputs.

5. Notation differences

In the preceding text we used the notation most often seen in systems and signals analysis, however when the differences described are implemented and we perform deep learning convolution, we usually use the following notation:

• \(h(t)\) is called the weights and usually denoted with a \(w_i\) with the subscript \(i\) specifying a \(t\) value.
• \(x(t)\) is still the input (to a convolutional layer) and is usually denoted \(x_i\) with \(i\) specifying a value for \(t\).
• \(y(t)\) is still the output (to a convolutional layer) and is sometimes denoted \(y_i\) or simply \(f\), again with \(i\) specifying the \(t\) value if given.

So that was a quick look at how the basic systems and signals idea of convolution relates to the convolution operation used in convolutional neural networks. I hope that was useful or at least looked cool. If you think I am wrong about something, please do get in touch so I can correct it :).

PS: if you want any of the source code used to create the visualizations, have a look at my github repo ExperimentK under the /Posts folder.